We have discovered how gravitational fields work and some facts about them, today we continue to expand the theories that use the similar ideas, from electricity to gravitation. Gravitational potential energy is a very familiar topic in mechanics, so this is an easy post. Aside from the main point, let's pick up the little tail from the last post.
What I should know
Read Gauss' law in gravitation.
When a mass falls into the hole that penetrates the centre of a uniform sphere, it does simple harmonic motion.
Potential energy is a scalar quantity. For a system of particles, energies do never cancel each other but only transform or are transformed into/from other types of energy. The amount of energy that a system has is an algebraic sum. Potential energy should equal to the negative of the work done by a force from a reference point to this point. It reflects the relationship between both objects, while potential only reflects the property of one.
Imagine Earth as a uniform sphere
Simple harmonic motion
(1) I certainly will not say that when you jump into the earth the volcano erupts and you'll be burnt out and so on. (2) The data calculated through this is not accurate.
We have discussed that within a uniform sphere, the gravitational field exerted by it is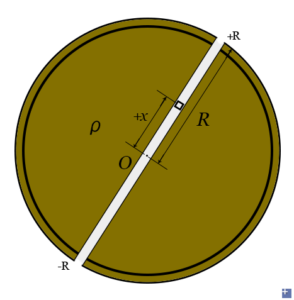
\[\vec{\mathrm{g}}=\frac{Gm}{R^{3}}\vec{r}\]
The radial distance vector 
points outward while the field 
points inward.
So if a test object m0 falls into a tunnel that penetrates the centre of the earth, it will be affected by the gravitational force due to the field, so its motion is \[-\frac{Gmm_{0}}{R^{3}}r=m_{0}a\]
This satisfies the requirement of simple harmonic motion, letting x be the displacement, this becomes \[\ddot{x}+\frac{Gm \, m_{0}}{R^{3} \, m_{0}}x=0\] From the equation we immediately know \[k=\frac{Gm \, m_{0}}{R^{3}}, \, \, \, \, \omega =\sqrt{\frac{Gm}{R^{3}}}\]
Since the test mass is initially on the surface level, the phase shift is zero, the solution of it is
\begin{align*}
&\mathrm{displacement} \, x=R\mathrm{cos}\omega t\ & \\
&\mathrm{velocity} \, v=\dot{x}=-\omega R \mathrm{sin}\omega t & \\ &\mathrm{acceleration} \, a=\ddot{x}=-\omega ^{2} \, x
\end{align*}
If we plot the average data of Earth in to it, then the period of one turn is 84 minutes, the time needed to travel from the ground to the opposite ground is 42 minutes.
We know the simple harmonic motion is a projection on one perpendicular axis of a uniform circular motion. So the path along this circular motion is just the Earth circle (Earth is considered sphere). A low-Earth satellite has a circular radius R+h ~ R. So the x-axis displacement of its orbit is like the displacement of this tunnel.
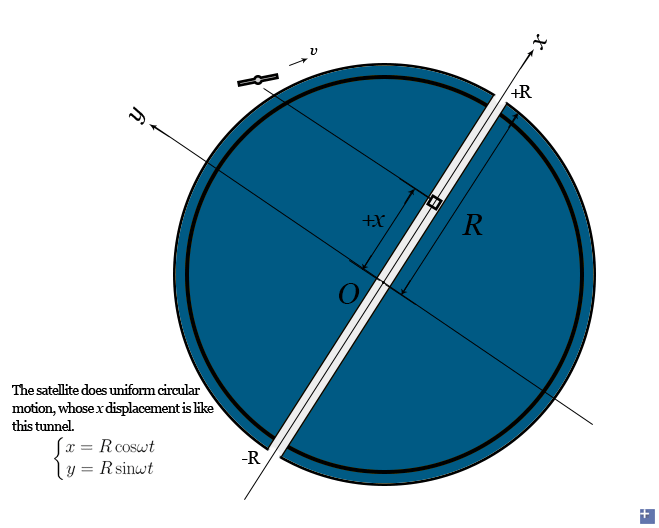
Energy considerations
Since we have assumed this whole process as a simple linear oscillator, other knowledge can also be transferred to this topic, such as elastic potential energy and kinetic energy.
According to the definitions of the oscillator, its kinetic energy is entirely associated with the accelerating mass: \[K=\frac{1}{2}mv^{2}=\frac{1}{2}kR^{2} \, \mathrm{sin^{2}\omega t}\]
Our "spring restoring force" is the gravitational force within the sphere. The potential energy is entirely associated with the spring (Earth): \[U=\frac{1}{2}kx^{2}=\frac{1}{2}kR^{2} \, \mathrm{cos}^{2} \omega t\]
Thus we can say this falling process is a transformation between two types of energy, the total mechanical energy is conserved, \[E=U+K=\frac{1}{2}kR^{2}\]
- When t=0, which means on the surface of Earth, the mass has lowest kinetic energy and greatest potential energy \[E=U=\frac{1}{2}kR^{2}=\frac{Gmm_{0}}{2R}\]
With respect to centre of Earth being the zero potential reference. We will return to this result later.
Damped process
Taking the resistance into account, this swinging won't last forever, so the mass will do the damped simple harmonic motion.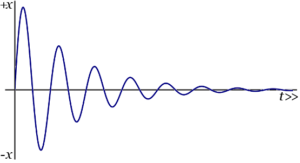
And people also know that Earth is not a uniform body, the density at the centre is greater than outer. For the 42 minutes, it should be a little bit shorter than that.
Potential
Potential energy
As we saw, potential energy is relative. The numerical expression of potential energy might differ if we change the reference, but if we have two points, the difference between them does not change. From position i to position f, the potential energy difference of a particle is \[\Delta U=U_{f}-U_{i}=-W_{\texttt{from} \, i \, \texttt{to} \, f}\]
W is the work done by the gravitational force/field. \[W_{if}=\int_{i}^{f}\vec{F}\cdot d\vec{s}\]
We often assign position i be the position where potential energy is zero, and infinitely far. So the potential energy can be written as \[U=-W_{\infty f}\]
If we escape the gravity, we will remain in equilibrium and travel forever. If not specifying, potential energy and potential are with respect to infinity being zero potential (energy) reference.
Gravitational potential
If we don't want to take care of the test particle, we can eliminate it, by simply dividing the potential energy by the mass of the test particle. Therefore, potential is independent of the mass. Letting V be the potential, so we can define V=U/m0 and \[\Delta V=V_{f}-V_{i}=-\frac{W_{if}}{m_{0}}\]
It means the gravitational potential energy difference of a unit mass.
We have noted that the work done by gravity is gravitational force times displacement, and gravitational field is just the force divided by mass, thus \[V_{f}-V_{i}=-\int_{i}^{f}\vec{\mathrm{g}}\cdot d\vec{s}\]
If choosing the potential Vi at position i to be zero, then \[V=-\int_{i}^{f}\vec{\mathrm{g}}\cdot d\vec{s}\]
Particle
With the reference being infinity, the displacement of the particle is from infinity to centre, the radial vector is along the increasing r axis, so their dot product should be negative.
\begin{align*}
V&= -\int_{\infty}^{r}\vec{\mathrm{g}}\cdot d\vec{s} \\
&=-\int_{\infty}^{r}\frac{-Gm}{r^{2}}dr \\
&=Gm\int_{\infty}^{r}\frac{1}{r^{2}}dr \\
&=-\frac{Gm}{r}
\end{align*}
Discrete points
Unlike force or field, gravitational potential energy and potential are scalar quantities, so for a system, their total potential is an algebraic sum.
\[V=-\sum_{i} V_{i}=-G\sum_{i}\frac{m_{i}}{r_{i}}\]
Continuous points
The integration over these points are still scalar.
\[V=-\int dV=-G\int \frac{dm}{r}\]
A rod of uniform linear density λ of mass is infinitely long, let's find the potential at distance R.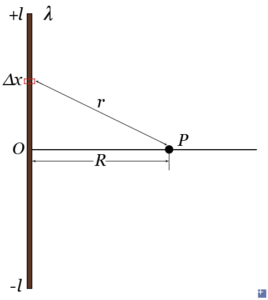
So we will select a mass element dx, and add all these elements together algebraically, from -l to +l.
\begin{align*}
V&=-G\int_{-l}^{ \, l}\frac{\lambda dx}{r} \\
&=-G\lambda\int_{-l}^{ \, l}\frac{ dx}{\sqrt{R^{2}+x^{2}}} \\
&=-G\lambda \, \mathrm{ln}\left (\frac{l+\sqrt{R^{2}+l^{2}}}{-l+\sqrt{R^{2}+l^{2}}} \right ) \\
&\xrightarrow[l \, \textrm{both sides}]{\textrm{divide by}} -G\lambda \, \mathrm{ln}\left (\frac{1+\sqrt{\left (R/l \right )^{2}+1}}{-1+\sqrt{\left (R/l \right )^{2}+1}} \right )
\end{align*}
The length l approches infinity, so binomial theorem 
can be used on both square roots, then
\begin{align*}
&\approx -G\lambda \, \mathrm{ln}\left ( \frac{1+\frac{R^{2}}{4l^{2}}}{\frac{R^{2}}{4l^{2}}} \right ) \\
&=-G\lambda \, \left [\mathrm{ln}\left ( 1+\frac{R^{2}}{4l^{2}} \right )-\mathrm{ln}\left ( \frac{R^{2}}{4l^{2}} \right ) \right ]
\end{align*}
Another approximation 
then can be used to have \[\approx -G\lambda \, \left [\frac{R^{2}}{4l^{2}}+2\mathrm{ln}\left ( \frac{2l}{R} \right ) \right ]\]
The first term is a second-degree infinitisimal, so we discard it to have \[\approx -2G\lambda \, \mathrm{ln}\left ( \frac{2l}{R} \right )\]
We thus know we cannot select infinity as zero potential since it is infinite potential there, so we have to choose two points
\begin{align*}
V_{a}-V_{b}&=-2G\lambda \, \left [ \mathrm{ln}\left ( \frac{2l}{R_{a}} \right )- \mathrm{ln}\left ( \frac{2l}{R_{b}} \right ) \right ] \\
&=2G\lambda \, \mathrm{ln}\left ( \frac{R_{a}}{R_{b}} \right )
\end{align*}
Let R0 be that zero potential plate, the result is
\[V=2G\lambda \, \mathrm{ln}\left ( \frac{R}{R_{0}} \right )\]