New look of gravitational field
conservative, irrotational
If we are in First floor's hallway, and we want to go to the washroom located on the second floor, we have lots of paths to go there. We can take the elevator to the second floor's main hall, then go to the washroom; or we can go to the third floor to pick up stuff, then go to the second floor's washroom. It doesn't matter which path you choose, you still change your position from 1st floor to 2nd floor height, so your gravitational potential (energy) don't vary with the path you selected.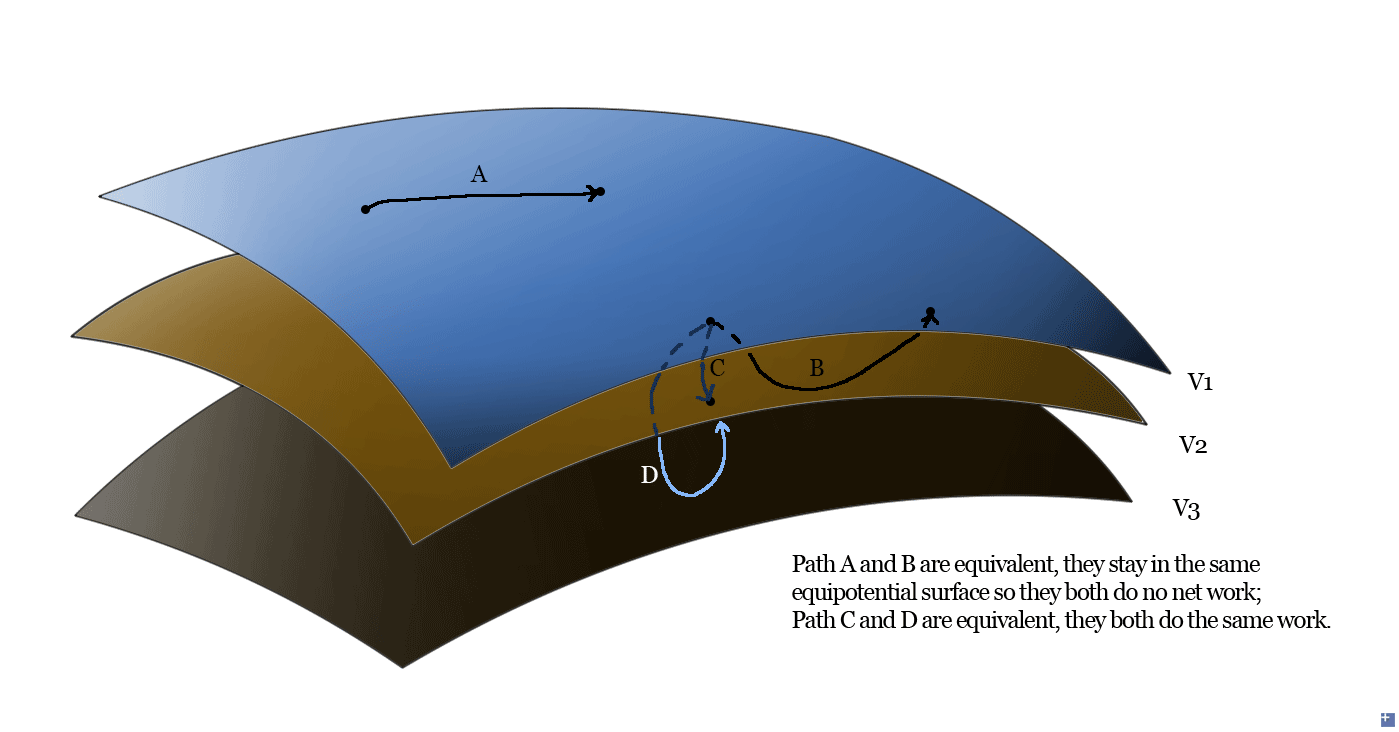
So we can say that gravitational fields are path independent. One symptom of such field is that if we do a circle, no net work is done. For example, we jump, reach the highest point, then fall down, return to the ground, the gravitational field does no work. Surfaces that have you same potentials (thus energy) are equipotential surfaces. In this case, gravitational field is said to be conservative: \[\oint \vec{\mathrm{g}}\cdot \mathrm{d}\vec{s}=0\]
According to Stoke's theorem \[\oint \vec{\mathrm{g}}\cdot \mathrm{d}\vec{s}=\iint \nabla \times \vec{\mathrm{g}}\cdot \mathrm{d}\vec{S}\]
Comparing two equations, we know gravitational field is irrotational: \[\ \nabla \times \vec{\mathrm{g}}=0\]
Original field of gravitational field
Math says there must be a scalar field corresponding to a vector field as long as it does not rotate. Gravitational field is vector field, so it has to have a similar original scalar field.
Suppose a test mass m0 moves through a differential displacement from one equipotential surface to another. The work being done can either be expressed as -m0dV or m0g·ds, equating them yields \[\mathrm{g} \, \mathrm{cos} \, \theta =-\frac{dV}{ds}\]
The cosine indicates direction, thus the component of gravitational field along a particular axis s is \[\mathrm{g}_{s}=-\frac{\partial V}{\partial s}\]
Which means \[\vec{\mathrm{g}}=-\nabla V\]
V is just like its mathematical name, potential field.
New look through gradient
Please refer to Fundamental theorem of calculus, as a pair of "derivative" and "antiderivative", they should meet \[\int_{L\left (\vec{a},\vec{b} \right )} \nabla V(\vec{s})\cdot \mathrm{d}\vec{s}=V(\vec{b})-V(\vec{a})\]
Assign a zero potential to the starting point, there is \[V=-\int_{L}\vec{\mathrm{g}}\cdot \mathrm{d}\vec{l}\]
Where L is an abtrary path, starts from a zero potential point i, ends at final position f. Vector element dl points along the direction of increasing axis (direction of positive work).
Poisson's equation
Recall that \[\nabla \cdot \vec{\mathrm{g}}=-4\pi G\rho\]
So \[\Delta V=\nabla \cdot \left ( \nabla V \right )=4\pi G\rho\]
Which is a kind of useful partial differential equation.
Calculate the potential
Infinite rod
We assign a zero potential point r0. Must be aware 
that in my image, the increasing radial axis r is towards right, also, the gravitational field points left.
We know that the gravitational field due to an infinite rod is \[\mathrm{g}=\frac{2\lambda G}{r}\] So at distance r, the potential difference is
\begin{align*}
V& =-\int_{r_{0}}^{r}\vec{\mathrm{g}}\cdot \mathrm{d}\vec{r}\\
&=\int_{r_{0}}^{r} \frac{2\lambda G}{r}\mathrm{d}r \\
&=2\lambda G\int_{r_{0}}^{r} \frac{\mathrm{d}r}{r} \\
&=2\lambda G \, \mathrm{ln}\left ( \frac{r}{r_{0}} \right )
\end{align*}
Infinite sheet
A sheet has a surface density of σ, the direction of increasing axis is still right.
\begin{align*}
V&=-\int_{r_{0}}^{r} -2\pi G\sigma \mathrm{d}r \\
&=2\pi G\sigma \left ( r-r_{0} \right )
\end{align*}
Shell
A shell has a radius of R, when outside the shell r≥R, infinity is zero potential point,
\begin{align*}
V&= -\int_{\infty}^{r}\frac{-Gm}{r^{2}}\mathrm{d}r \\
&=-\frac{Gm}{r}
\end{align*}
When inside the shell r<R, infinity is zero potential point, it becomes more complicated since now the path will pass two portions: outside and the inside part, and they have different fields.
\begin{align*}
V& =-\int_{\infty}^{r}-\mathrm{g}(r) \mathrm{d}s \\
&=-\left (\int_{\infty}^{R} - \mathrm{g}(r) \mathrm{d}s+\int_{R}^{r}-\mathrm{g}(r) \mathrm{d}s \right ) \\
&=-\int_{\infty}^{R}\frac{-Gm}{r^{2}} \mathrm{d}s-\int_{R}^{r}0 \, \mathrm{d}s \\
&=-\frac{Gm}{r}
\end{align*}
Sphere
A sphere has a radius of R, when outside the shell r≥R, infinity is zero potential point, it is the same as a shell
\[V=-\frac{Gm}{r}\]
When the point is inside the sphere, two different gravitational field amplitudes also need to be considered
\begin{align*}
V&=-\int_{\infty}^{r}-\mathrm{g}(r) \mathrm{d}s \\
&=-\left (\int_{\infty}^{R}-\mathrm{g}(r) \mathrm{d}s+\int_{R}^{r}-\mathrm{g}(r) \mathrm{d}s \right ) \\
&=-\int_{\infty}^{R} \frac{-Gm}{r^{2}}\mathrm{d}r-\int_{R}^{r}\frac{-Gm}{R^{3}}r\mathrm{d}r \\
&=Gm\left [ -\frac{1}{r} \right ]^{R}_{\infty}+\frac{Gm}{R^{3}}\left [ \frac{1}{2}r^{2} \right ]^{r}_{R} \\
&=\frac{Gm}{2R}\left ( \frac{r^{2}}{R^{2}} -3\right )
\end{align*}
Noticed if we calculate the potential energy difference of a test particle m0 between the surface and the centre of Earth using this equation, we will find \[U_{\mathrm{surface}}-U_{\mathrm{centre}}=\left ( -\frac{Gmm_{0}}{R} \right )-\left (- \frac{3Gmm_{0}}{2R} \right )=\frac{Gmm_{0}}{2R}\]
References
Halliday, David, Robert Resnick, and Jearl Walker. Fundamentals of physics. New York: Wiley, 2001.
Journal of Nanchang University (Engineering & Technology). Extension of Gauss's Law and Circuital Law in the Universal Gravitation Field. Nanchang University, 2008.
Xuesheng Li, Gauss' Law in Gravitational Field. Shandong University Physics Campus.
Image credits to Im cleoold.
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.