In mechanics, switching reference frames is a prevalent way to simplify questions, as long as it becomes easier. Centre-of-momentum reference frame, or centre-of-mass, zero-momentum frame, is an interesting alternative method to solve such problems. Do you feel tired of "conservation of linear momentum"?
Basically, such reference frames involve centre of mass, please review the definition:
Position of the CM: $ \mathbf{r}=\frac{1}{M}\sum_i m_i \mathbf{r}_i $
Velocity of the CM: $ \mathbf{v}=\frac{1}{M}\sum_i m_i \mathbf{v}_i $
So does the acceleration. Where big M is the total mass. We already know if a system of objects is not being acted by extra external forces throughout the entire motion (forces don't change), the path of the centre of mass is not altered. For two balls, no matter how they collide with each other, the point of CM always remains the same motion as long as we do not push them.
Path remains the same
Question: Two balls with masses m1 and m2 are shown. m1 has an initial velocity v1 while m2 is at rest. When they meet, a completely inelastic collision happens so they stick together. What's their final velocity?
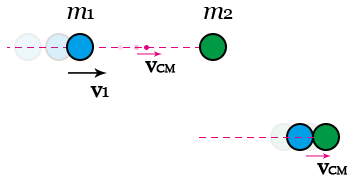
So the two balls just collide with each other, which means only internal forces are present. This is that the path of CM doesn't change during this process, so vCM=vCM'. We then know the two balls stick together after this, so they have a common velocity, which is v'=vCM'.
Before the collision, note m2 has no velocity
\[\mathbf{v}_{\mathrm{CM}}=\frac{\sum m_i \mathbf{v}_i}{\sum m_i}=\frac{m_1 \mathbf{v}_1 +m_2 \mathbf{v}_2}{m_1 + m_2}=\frac{m_1 \mathbf{v}_1}{m_1 + m_2}\]
After the collision, two objects have the same velocity
\[\mathbf{v}_{\mathrm{CM}}'=\frac{m_1 \mathbf{v}' +m_2 \mathbf{v}'}{m_1 +m_2}\]
Equating them has \[m_1 v_1 =(m_1 +m_2)v'\]
Net momentum is zero
The method above is related to the position of CM, no momentum is used. How do we make some momentum to it?
If we choose the centre of mass as the reference frame, for velocity, there is
\[v'+V_{\mathrm{CM}}=v\]
object's velocity relative to the CM + CM's velocity relative to the ground = object's velocity relative to the ground
Total momentum: \[P'=\sum_i m_i v_i ' =\sum_i m_i (v_i - V_\mathrm{CM})=\sum_i m_i v_i - \sum_i m_i V_\mathrm{CM}\]
Where $ V_\mathrm{CM}=\frac{\sum_{i'} m_{i'} v_{i'}}{\sum_{i'} m_{i'}} $
After some algebra, note i and i' mean different terms, but have the same number, finally
\[P'=0\]
This powerful identity says within a CM inertial reference frame, the net momentum is zero. Let's do that question again.
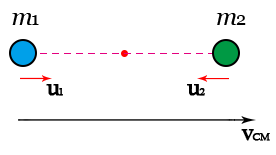
In the CM's frame (treat CM as stationary one), m1 is approaching the CM from the left and m2 is approaching the CM from the right. Since
m1's velocity relative to the CM + CM's velocity relative to the ground = m1's velocity relative to the ground \[u_1+v_\mathrm{CM}=v_1\]
So does m2. Thus, keep the sign,
\[\left\{\begin{matrix} m_1 u_1 +m_2 u_2 =0 \\ u_1 =v_1 - v_{\mathrm{CM}} \\ u_2 = -v_{\mathrm{CM}} \end{matrix}\right.\]
Which yields $ m_1 v_1 =(m_1 +m_2)v_{\mathrm{CM}} $
Question: The person holding a ball who has an initial velocity v0 at angle θ jumps, when he arrives at the highest point, he throws out the ball to his back at a relative velocity u so he will land farther. Suppose his mass is M and the ball m. How much farther will he land than not throwing that ball?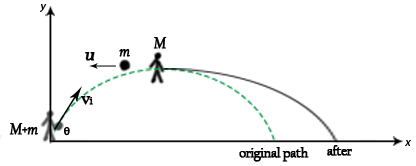
In this question, throughout his entire motion, the only external force acting on them is gravity, which always points downward so it is not changing. Thus the path of the CM does not vary even though he throws the ball, and still is the original parabola. The question becomes the distance between his landing position and the position of the CM >> his displacement relative to the CM.
In the frame of the CM, let V be the velocity of the person, v of the ball.
Note u and V are opposite.
\[\left\{\begin{matrix} mv+MV=0\\ v=V+(-u) \end{matrix}\right.\]
Also, $ v_0 \, \mathrm{sin}\theta =gt $
Thus \[\Delta x=Vt=\frac{mu}{M+m}\frac{v_0 \, \mathrm{sin}\theta }{g}\]
Not a lot of calculations are needed.
