Initially, Gauss investigated the pattern of gravity and developed "Gauss' law for gravity" but unexpectedly it turned out to be a useful law in electrostatics, leaving this gravitation law "unknown" and seemingly useless. Gauss' law for gravity is completely an equivalent law as Newton's law of universal gravitation, let's start from Newton's law and see what we can find.
What I should know
Gauss' law of classical electromagnetism: \[\Phi =\frac{q}{\epsilon _{0}}\]
Gravitational field: A vector. It has the same magnitude as that of the gravitation force acting on a one-kilogram mass, the same direction as that force. Its unit is N/kg.
Field lines: Their tangents should point towards the direction of the gravitational force. They start from infinitely far and should point towards this object like a negatively charged electron. Field lines do not intersect or loop. The density of lines represents the strength of the gravitational field.
Gravitational flux: The product of the gravitational field at this position and the normal of this piece of area. \[\Phi =\vec{\mathrm{g}} \cdot \vec{S}=\mathrm{g}S \, \mathrm{cos}\theta\]
- normal vector: It has the same direction as the outer normal of the surface.
Newton's law in Gaussian form
For comparison, use this substitution: \[G=\frac{1}{4\pi g_{0}}\]
Then the gravitational field of m is \[\vec{\mathrm{g}}=\frac{1}{4\pi g_{0}}\frac{m}{r^{2}}\hat{r}\]
where 
is a unit vector that points to the mass.
So the total flux of the gravitational field through an arbitrary closed Gaussian surface should be \[∯\vec{\mathrm{g}}\cdot \mathrm{d}\vec{S}= ∯\frac{1}{4\pi g_{0}}\frac{m\hat{r}}{r^{2}}\cdot \hat{n} \, \mathrm{d}S=\frac{m}{4\pi g_{0}} ∯\frac{\hat{r}}{r^{2}}\cdot \hat{n} \, \mathrm{d}S\]
In order to use solid angle, we have to let 
point outside instead of into the centre, which means switching it opposite, so it becomes
\[\frac{-m}{4\pi g_{0}} ∯\frac{\hat{(-r)}}{r^{2}}\cdot \hat{n} \, \mathrm{d}S=\frac{-m}{4\pi g_{0}} ∯\mathrm{d}\Omega =\frac{-m}{4\pi g_{0}}4\pi\]
Thus \[\Phi =∯\vec{\mathrm{g}}\cdot \mathrm{d}\vec{S}=\frac{-m}{g_{0}}=-4\pi Gm\]
This is Gauss' law for gravity. Note that surface S must be a closed Gaussian surface, and m is the total mass enclosed in that surface, for example, earth's surface. Here the flux Φ is a negative quantity, so it is inward.
This tells us an important message that no matter how much kilograms are placed outside the enclosed surface we choose, the net flux through the surface does not change. Therefore, we can actually have infinite choices of Gaussian surfaces when dealing with problems. We will use this property later.
Gravitational field is sunken
We can consider the mass distribution over a solid body as a triple integral, so the equation becomes
\[∯\vec{\mathrm{g}}\cdot \mathrm{d}\vec{S}=\frac{-∭\rho \, \mathrm{d}V}{g_{0}}\]
Divergence theorem of calculus states \[∯\vec{\mathrm{g}}\cdot \mathrm{d}\vec{S}= ∭\nabla \cdot \vec{\mathrm{g}} \, \mathrm{d}V\]
So the sink of gravitational field is
\[\nabla \cdot \vec{\mathrm{g}}=-\frac{\rho }{g_{0}}=-4\pi Gm\]
This means all the field lines must gather at the mass.
Newton's law of gravitation
So that it is easy to show that the gravitational field due to a particle m is \[\vec{\mathrm{g}}=\frac{1}{4\pi g_{0}}\frac{m}{r^{2}}\hat{r}\]
Similar methods of proof will be used later, so I skip the derivation for now.
So the magnitude of the gravitational force due to m on another mass is \[F=\frac{1}{4\pi g_{0}}\frac{mm_{1}}{r^{2}}=\frac{Gmm_{1}}{r^{2}}\]
Planar symmetry and cylindrical symmetry
Infinite sheet
The figure shows a portion an infinite big sheet with a uniform surface density of σ (kilogram per unit area), it does not contain unneutral charges. Let's find the gravitational field at distance r.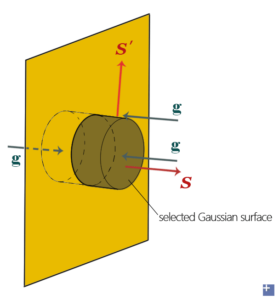
A useful Gaussian surface is a closed cylinder that pierces this surface and has two caps on each end. Must note that there are two directions from which field lines come into the sheet.
For this imaginary cylinder, if we rotate it along its central axis, we won't detect any shape difference. Thus, we conclude that all that come into the surface do not vary with the shape (we have assumed uniform density). As a result, we can take the out of the integral. For the flux, we find there are two parts: two ends and one body part. We find the normal of surface S' is perpendicular to the incoming field lines, since cos90°=0, there is no flux for every point on S'. The normal vector of cap S is right opposite to the field lines, and cos180°=-1, so
\[\Phi =2∯\vec{\mathrm{g}}\cdot \mathrm{d}\vec{S}=-2\mathrm{g} ∯\mathrm{d}S=-2\mathrm{g}S\]
The mass enclosed in that surface is simply σS, thus \[\Phi =-\frac{\sigma S}{g_{0}}\]
\[\mathrm{g}=\frac{\sigma }{2g_{0}}=2\pi G\sigma\]
Two infinite sheets
Two sheets are separated by a distance L and have surface densities σ1 and σ2.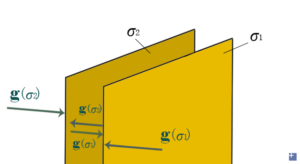
When σ1 and σ2:
If inside the open area, we can select an enclosed Gaussian surface between two sheets, that can be a cube or anything, then we find that this surface does not include any mass, therefore Φ=0. This means the field lines enter the area and then exit, leaving nothing. We can then conclude zero gravitational field here.
Must note: In electromagnetism, Gauss' law failed as the presence of non-symmetrical charge arrangements (eg: dipole), as a result, Φ=0 does not certainly imply E=0. However, there is symmetry in this question, so we can have the conclusion above. Otherwise, we will use the principle of superposition.
In the outside, we can use the similar cylindrical model, note that the field lines inside the open stay in the Gaussian surface. \[(-\mathrm{g}S)+(-\mathrm{g}S)=-\frac{\sigma S+\sigma S}{g_{0}}\]
\[\mathrm{g}=\left\{\begin{matrix} \frac{\sigma }{g_{0}}=4\pi G\sigma&,\textrm{outside both sheets}\\ 0&,\textrm{between two sheets} \end{matrix}\right.\]
Infinite rod
A rod has a uniform linear density of λ (kilograms per unit length), let's find the gravitational field at distance r.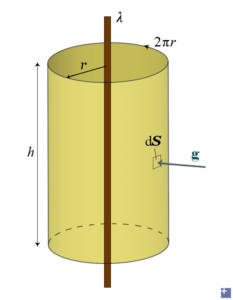
Imagine a Gaussian surface of a cylinder. It has a radius of r and thus a circumference of 2πr. We find that the incoming field lines are always perpendicular to the normal of the side, so we can again get rid of the integral. As for the two caps, there are no flux passing. The mass of this enclosed rod is then density times length.
\[\mathrm{g}(2\pi rh)\mathrm{cos180°}=-\frac{\lambda h}{g_{0}}\]
\[\mathrm{g}=\frac{\lambda }{2\pi g_{0}r}=\frac{2\lambda G}{r}\]
Infinite cylinder
Similar as above, but now it is a solid cylinder with a uniform density ρ (kilograms per unit volume).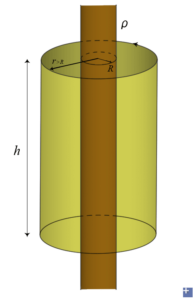
The clue to this problem is the uniform density. Inside the cylinder, If we select a Gaussian surface, the mass is varying with the change of radius. We mark the mass enclosed as m', using Gauss' law \[-\mathrm{g}S=-\frac{m'}{g_{0}}\]
For r<R, there is \[\mathrm{g}(2\pi rh)=\frac{\pi r^{2}h\rho }{g_{0}}\]
Starting from the surface of the cylinder, which means r≥R, the enclosed mass stops changing, and sticks to πR2hρ, that is \[\mathrm{g}(2\pi rh)=\frac{\pi R^{2}h\rho }{g_{0}}\]
\[\mathrm{g}=\left\{\begin{matrix} \frac{\rho }{2g_{0}}r=2\pi G\rho r&, r< R\\ \frac{R^{2}\rho }{2g_{0}r}=2\pi GR^{2}\rho \frac{1}{r}&,r\geq R \end{matrix}\right.\]
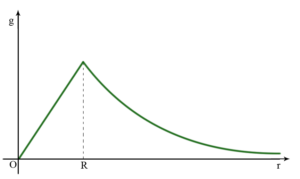
Spherical symmetry
Spherical shell
A uniform spherical shell has a mass of m. On or outside its shell, we choose a Gaussian surface S2 or S3.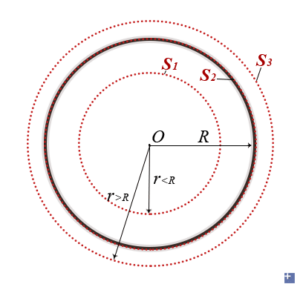
The total mass enclosed by this surface is still a defined number m no matter the increase of r. So r being the variable, there is \[-\mathrm{g}(4\pi r^{2})=-\frac{m}{g_{0}}\]
As for r<R, the gravitational field is 0. I am not quite convinced by the Gaussian solution to this topic since there is no explicit symmetry inside this shell. Please refer to Shell theorem or the Calculus solution.
\[\mathrm{g}=\left\{\begin{matrix} \frac{1}{4\pi g_{0}}\frac{m}{r^{2}}=\frac{Gm}{r^{2}}&,r\geq R \\0&,r< R \end{matrix}\right.\]
However, this reveals that a shell of uniform mass attracts a particle that is outside the shell as if all the shell's mass were concentrated at the centre of the shell. This is a convenient way to prove it.
Sphere
All the same, but now it is solid and a mass of m.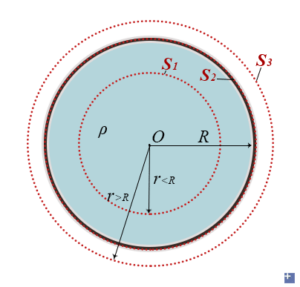
For r≥R, we can use the same idea as the hollow shell since the mass is not changing, which is \[-\mathrm{g}(4\pi r^{2})=-\frac{m}{g_{0}}\]
We thus know on the surface, the sphere attracts particles as though from a concentrated centre. If we choose a Gaussian surface S1, the enclosed portion of mass will do so, we let m' represent this part of mass. Since the mass is distributed uniformly throughout the volume, we have \[\frac{m'}{\frac{4}{3}\pi r^{3}}=\frac{m}{\frac{4}{3}\pi R^{3}}\]
\[m'=m\frac{r^{3}}{R^{3}}\]
Substitute this result into the last equation :
Finally, \[\mathrm{g}=\left\{\begin{matrix} \frac{1}{4\pi g_{0}}\frac{m}{r^{2}}=\frac{Gm}{r^{2}}&,r\geq R\\ (\frac{m}{4\pi g_{0}R^{3}})r=(\frac{Gm}{R^{2}})r&,r<R \end{matrix}\right.\]
Where 
is a constant, this reveals if a particle falls into a tunnel that penetrates the uniform sphere, it will do simple harmonic motion.
References
Halliday, David, Robert Resnick, and Jearl Walker. Fundamentals of physics. New York: Wiley, 2001.
Journal of Nanchang University (Engineering & Technology). Extension of Gauss's Law and Circuital Law in the Universal Gravitation Field. Nanchang University, 2008.
Xuesheng Li, Gauss' Law in Gravitational Field. Shandong University Physics Campus.
Image credits to Im cleoold.
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.